|
TRANSFORMATION
|
|
| Atom, input, resonance expansions and the energised atom ... |
How many decades will it be before the classical biologist and
the non-fractal mathematical physicist are
persuaded that
the replication of DNA and duplication of the cell is,
ultimately, realisation and embodiment
of quantum
systems self-organisation and information packing?
We need a new beginning really and to identify what
will inform and drive the new understanding that the quantum foundation of living systems research seems to offer. Perversely
we work with the most complex of systems, the cell, from the most complex elaboration of such systems, man, and rely
in part on working backwards and, in modelling, starting at the end.
|
|
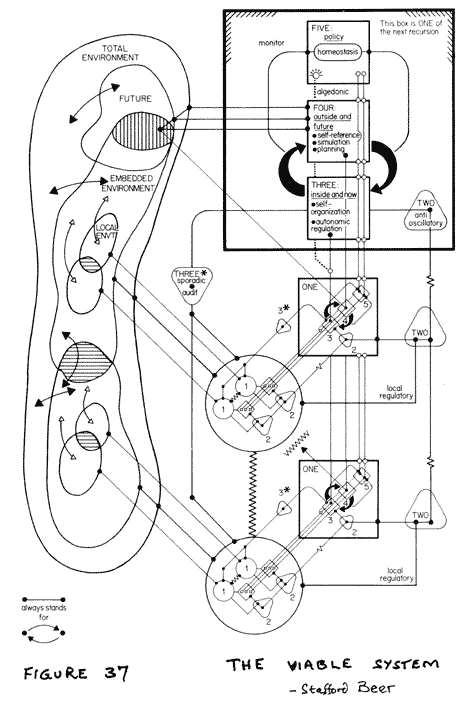
| Beer's Viable System Model - Nature as the fundamental referent of cybernetics and systems theory |
Systems thinking
In the light of the human genome mapping project findings,
post-genomic life science has had to quickly shift focus from the old ground of genes and proteins and, in large part, has
moved to the new ground of 'systems' in the hope that in so doing the genome, transcriptome and proteome (amongst
many other '-omes' or populations of bio-components) will complete the mapping of all activity and explain the
real role of 'Junk DNA' by default.
Some of the earliest thinking and models in systems
theory come from the field of cybernetics, a field which is, in the minds of most people, most immediately associated with
hard machines, robots and AI, although in fact all first working and modelling was derived from natural systems analysis,
e.g., neural working and networks, as is readily evidenced by W Ross Ashby's contribution to the foundations
of cybernetics in his first book Design for a Brain. Above also is illustration by Stafford Beer, the
father of British cybernetics and systems theory, of his own Viable System Model, itself a very general abstraction based
on his own analysis of living systems organisation. The model presented here should in fact serve to illustrate
the limits of sapient robotics and 'hard AI'.
As W Ross Ashby in An Introduction
to Cybernetics (1956) explains, cybernetics is principally 'functional and behaviouristic', effectively
seeking to provide a general and dynamic structuralism for systems process analysis. Beyond providing a common
language by which some unity of principle might be realised between a variety of phenomena and, therefore, disciplines,
cybernetics, Ashby claimed, should come into its own particularly when dealing with 'complex systems', i.e.,
systems 'that just do not allow the varying of only one factor at a time - they are so dynamic and interconnected that
the alteration of one factor immediately acts as cause to evoke alterations in others, perhaps in a great many others'
... 'Such systems are, as we well know, only too common in the biological world! ...[]... It is chiefly when the systems
become complex that the new methods [of cybernetics] reveal their power'.
This is a wonderful vision for the
power of cybernetics and perfectly illustrates that it is an emergent or second order discipline, as is complexity
theory itself, but as Ashby reported, our understanding then of the nature of complexity was necessarily naive and the
philosophical and methodological shift from hard systems dogma and movement towards the analysis of complex systems only
in its infancy: 'Until recently science tended to evade the study of such systems ... but science today is also
taking the first steps towards studying "complexity" as a subject in its own right.'
It
is interesting to note that the imagination of this founding contributor to systems or cybernetics theory was implicitly
geometric, as indeed it needs to be, systems analysis naturally requiring that the functionalities and behaviours identified are
themselves mapped or modelled in space and time, in the abstract and in relation to the particular circumstance of a found
reality.
Ashby offers his interpretation of geometry achieving some transcendance by the power
of its abstraction allowing the modelling of any geometric form or system and, transformed by this transcendance becomes,
like cybernetics and complexity theory, its own second order, emergent discipline.
'There was a time when
"geometry" meant such relationships as could be demonstrated on three-dimensional objects or in two-dimensional
diagrams. The forms provided by the earth - animal, vegetable and mineral - were larger in number and richer in properties
than could be provided by elementary geometry. In those days a form which was suggested by geometry but which could not be
demonstated in ordinary space was suspect or inacceptable. Ordinary space dominated geometry.' (Ashby's italics).
'Today the position is quite different. Geometry exists in its own right, and by its own strength.
It can now treat accurately and coherently a range of forms and spaces that far exceeds anything that terrestrial space can
provide. Today it is geometry that contains the terrestrial forms, and not vice versa, for the terrestrial forms are
merely special cases in an all-embracing geometry'.
'The gain achieved by geometry's development hardly
needs to be pointed out. Geometry now acts as a framework on which all terrestrial forms can find their natural place,
with the relations between the various forms readily appreciable'.
When we ask what informs Ashby's
mathematical and very prescient 1956 advocacy for the coming into being of an 'all embracing' workable 'systems
geometry' we do not have to look too far as there is only one reference to a significant and explicitly
mathematical work in the bibliography of An Introduction to Cybernetics and this is to the work of N Bourbaki,
1951, Theorie des Ensembles, essentially a fundamental geometric contribution to set - and therein to systems
and dynamical systems - theory.
The work of the Bourbaki school cannot be dealt with here beyond pointing
up the direct lineage this gives us to the geometry of today that has emerged, in part, from the Bourbaki working (which
was itself effectively a French parallel to the Principia Mathematica work of Russell and Whitehead, i.e., both
seeking logical foundation) and which Ashby, no doubt, would be thrilled to see. The link here is that participant
and contributor to the group working of the Bourbaki school was Szolem Mandelbrot ... and we all know whose
Uncle he was ...
So, in essence, Ashby's cybernetic 'systems' thinking was strongly informed by the
elaborations of set theory developed to deal with complex dynamic sets or systems, one of whose founding contributors
went on to inspire his nephew as to the possible value of studying mathematical obscurities such as those in which he
himself was involved ...
|
|
| Fractal 'Mandelbulb' image |
Complexity
Complexity science has made much progress and we today recognise that the study of
living systems is the study of complex quantum systems (atoms) self-organising to give rise to complex atomic systems (molecules),
which in turn self-organise to give rise to the complex molecular systems that combine to constitute the living system
that is the cell, complexing from there to give rise, ultimately, to the complex system that is an organism such as man.
This manifold embedding of complex systems within larger complex emergent systems acts to diminish the determinism
fundamentally inherent in deterministic chaos and instead raises the possibility of transcendant effect, bottom up or top
down, where the interplay of system levels can itself perhaps act as a feedback mechanism. The pathway, if you
like, for 'real' chance, the dimension that Bohm insisted always be considered, if not immediately included, in our
modelling of complex systems. Sadly, we know little as yet - hence the need for this site - about self-organising,
complex atom-based quantum systems working far-from-equilibrium and which are continuous in both the instantaneous moment
and over evolutionary time.
The real driver of complex systems is their 'sensitivity' whereby complex
dynamical systems respond non-linearly, i.e., with damping or amplification, to perturbations. As research and application
continue to only ever add to the list of phenomena we have found to be chaotic and complex - indeed, 'Non-chaotic systems
are very nearly as scarce as hen's teeth, despite the fact that our physical understanding of nature is largely based
upon their study' (Ford, 1983, quoted in Satinover, 2001) - and, therefore, fractal, it becomes ever more appropriate
to work from the extreme of the philosophy, to accept a fractal universe and, therefore, the universe as a complex, fractally
structured 'sensitive' system. This is not surprising when we recall that the motive laws are field laws, acting
with geometric or power law behaviour, intrinsically non-linear - twice the distance, quarter the power, etc., however you
wish to express it. It is a sensitive universe? By our own adopted logic of a fractal universe then, too, all
that is within it is 'sensitive' - open and reactive and capable of complex and elaborated response.
Both non-linear types of response require and are the result of resource reservoirs being available to generate
their effect, these reservoirs themselves being subject to sensitive control, this effectively making an holistic suprasystem
by the embedding of sensitive systems.
Beyond living systems and, therein, man, as exemplar
for complex, non-linear, far-from-equilibrium, dynamical systems, for biological knowledge further complexity
lies mainly in its own sheer volume of data, the incompleteness of that data set and the arbitrary aspect introduced
by 'selection' in molecular biology and evolution. We have a vast catalogue of dancers and some
of their behaviours and history, but we do not know the 'why' of their dance and how the apparently random is
accommodated and made useful.
The larger complexity is socio-political, in so far as ~50 years has been
spent in study of <3% of the genome - around which all our health and pharma industries are built - and classical biology has
somehow now to justify its own continuance (beyond the sheer cataloguing of data) by quickly getting to grips with the 97%
of material still requiring functional description.
Incompleteness also plays a part in terms of the
physical approach to biological complexity in that, for the physicists, complexity has closer definition and is about
more than just 'complicated' systems once deterministic chaos and information theory are introduced. Indeed,
it might be suspected that living systems present the first ground for our understanding of continuous systems. At
fundament living systems present the possibility of understanding a new and different, somehow inverse physics,
effectively broadening the current remit of physical theory.
There is also a reported incompleteness by
virtue of the slow take-up of fractal geometry in application to the foundations of quantum theory, as was pointed out by
Palmer (2009) and confirmed by Coecke (2009) (FGCT pages to come will cover this), yet this percieved shortfall is in
spite of all the quantum chaos research and application evidenced, for instance, by the ArXiv archive which
listing of such papers extends back to 1993 at least. Something is awry there, surely?

Ending the 'machine' idea
It
is required that we abandon the idea of living systems as any sort of 'machine'. The term is really born
of the scientific movement to a technological triumphalism, when the machine was seen as man's greatest invention
and the potential saviour of society, but machines we certainly are not. As the idea of living systems as machines fades
so, as we now know, the idea of the gene fades and natural selection becomes description of a wide filter, at many scales
of length, time and phenomenology.
Machines do not generate new parts for themselves or by chance develop novel
pathways whereby the 'old parts' have to find new function. Machines do not regenerate themselves, every part
and atom, every seven to fifteen years - time estimates vary with respect to different tissue types and, consequently, overall
time to complete replacement. (Fifteen seems best to me - think about the folk you know at those ages - ~15, ~30,
~45, ~60 and ~75. We all know how someone can change dramatically with that same periodicity - from puberty and
first freedom, through the 'finding a mate and settling down' period to middle age, retirement and the 'later'
years ...).
Perversely circular it may be, but also machines are not self-organised quantum systems! They
do not have an idling function of self-reflection. They do not take generic comparators into consideration, they do
not emote, they do not think or feel, they do not evolve new solutions within an intelligent framework. They do not
search to understand. Indeed, they cannot 'understand', just as the cat must marvel at the facts of television
when you explain, but will never 'understand'. They are not autopoietic. They are not naturally and directly
dependent on and, therefore, sensitive to, their environment, nor are they curious as to how they themselves came into being.
Machines are not curious. They do not, of course, have any autonomy and cannot, therefore, be 'curious', cannot
freely explore the variety of possibilities that present themselves. They are not each the environment of another, although
the machines of man do provide more environments for living systems - there are few natural environments where viruses and
bacteria, seeds, lichens and mosses, for example, get to live in window putty.
That is not to say that such analogy
will no longer be useful, as, ironically, the gedanken model worked here will heavily demonstrate, but that's it, no more
after this (please, nicely)! It is, after all, 'process', as Whitehead understood it.
This point is also made by Satinover (2001):
'It might rather be the case that what we are getting a glimpse of now in artificial systems will show us the way to
discover much the same within ourselves - just as the development of neural networks shed the first clear light on how networks
of neurons work. It would be fine poetic justice, should our construction of thinking machines [i.e.,
quantum computers] that turn out to be not really machines at all enable us, for the first time in four hundred
years, to see from a scientific perspective that neither are we.' (My emphases, the italic to point
up the shared perception of the historic scale of this revolution for science).
Natural Computation
There is at
present a relatively small group of workers who strongly propose the cosmos as, essentially, some sort of computational system
- Seth Lloyd, David Deutsch, Vlatko Vedral and, perhaps, Stephen Wolfram. In so far as we find ourselves in the dynamic, i.e.,
disequilibrious, environment of an n-dimensional curved expanding and complex spacetime, all condensed matter and energy is
then in a constant state of tensional flux or state change and state change, to man, bespeaks computation or the means towards
it. Within that general frame, well yes, it is all computation - of a sort.
That general frame was made materially
pertinent in terms of the living state, as we saw earlier, by Adey and others working in bioelectromagnetics, who explicitly
sought to develop a dynamic physical understanding of living systems components and working. The quantum vision brings
components that are atoms, ions, protons and electrons and their working in the quantum self-organisation that is the protein
molecule. The translation of this bioelectromagnetic vision, or rather bringing it up to date in terms of the possible
computational powers therein already has description via Bray's (2009) book entitled 'Wetware', an exploration
of living systems functionality from the point of view of chemical computing.
More particularly, accepting that
living systems are exemplar for nano-systems components and working, we might perhaps more usefully then explore
the - or our - given circumstance, i.e., cellular dynamics and organisation, in order to better understand how these quantum
systems are in fact working.
To be developed within the site is a model of how otherwise we might see the familiar
objects and dynamics of the cell in its cycling and this brings us to a point of exquisite cross-over with questions
to do with quantum computing. Examination of the case will not, therefore, be prolonged here beyond simple acceptance
of the premise because the gedanken model allows us to very directly test current thinking on technological possibilities
and on the nature of the atom. The latter has its own page - ATOMS - whilst the technical aspects of quantum computing
are discussed later in QUBIT and NET.
The fundamental gedanken experiment here is to
model the human genome as a quantum system. In order to do so we need first to model the environment of the genome which
is, of course, the cell, from the point of view of physics, i.e., identifying the significant cell states, sub-system
behaviours and the ordinating sources for the dynamics.
Within that we can move on to
wonder at the functionality of the DNA embedded within the cellular system. With very basic construction and creative
interpretation of information from a number of disciplines, we can, in very few steps, raise a quite different model
for genome working.
> THE PHYSICAL CELL: FORM
|
|
| Clockwise from left: cloud chamber atomic collision trace, galaxy pair and lily cell flow ... |
|