|
Natural Mathematics
For the harmony of the world is
made manifest
in Form and Number,
and the heart and soul and all the poetry
of Natural Philosophy
are
embodied in the concept of mathematical beauty.
D'Arcy Thompson
'The
recognition of structured chaos
has been hailed as a third revolution,
worthy to be set alongside
the Newtonian
and quantum mechanical revolutions
which preceded it.'
John Polkinghorne, 'Reason and Reality' , SPCK 1991
A science-wide revolution?
Nearly twenty years
separate Polkinghorne's statement of revolution and the Royal Society acknowledgement of a 'radical paradigm shift' and
the juxtaposition of these statements serves, in Kuhnian principle, to illustrate both extremes of the process of scientific
revolution: from early support by a few significant workers in the field, to institutional statement, i.e., changing
the textbooks.
These are indications of revolution, but yet question remains as to what is really driving
this paradigm shift. 'Revolution' is a common call within disciplines, but by its very name we know it is spin-out
of something other driving forward, it is effect and not cause, indeed, revolution is a phase, neither a beginning or an end, just
a period of turbulence.
The Royal Society statement of the case is effectively confirmation that after only
two generations of development a chaotic reality is accepted by science and it is now only a matter of coming
to terms.
FRACTAL GEOMETRY AND CHAOS THEORY
|
|
| One version of the now iconic Mandelbrot Set - only realised by the power of computing ... |
Don't mention the Emperor's
new clothes ...
The revolution that dare not speak its name ...?
One has to wonder at
why this truly astonishing turn of events has been able to come about with no significant notice being given. Whilst
Benoit Mandelbrot has received a well-deserved share of prizes, there is a strange reluctance in some scientific
and, particularly, mathematic, communities to acknowledge the immensity of what he has achieved, either by playing down
his role as just developing the legacy of others or by playing down the profundity of fractal geometry itself. This
is a truly immense misjudgement by those who dismiss fractal working as trivial or so widespread as to have
lost all meaning or significance, but then fail to recognise that 'widespread' = universal - quite literally
universal, in this context. It is the geometry of our cosmos.
Nobody, it seems, is willing to risk their
Professorial pension by declaring the Emperor's new clothes to indeed be in place, of exquisite and fine self-organised
manufacture and possessed of a greater and more subtle beauty than almost any human mind could conceive. The 'Golem'
of classical biology is today made light, or rather is informed and animated by the transformation of light that underpins
the working system that makes man. Man's material form is made by the working of light and holography
renders form from light. I am camera, cinema and film?
And then there is nature, fabulous, 100-dimensional
(at minimum), nature, the task of understanding whose capabilities we cannot yet begin to fathom, though science has a made
a helpful start.
Much has been made of Wigner’s
historic observation on ‘the unreasonable effectiveness of mathematics’, but the statement today appears inadequate in light of the extraordinary transformation of vision that has been wrought in science by the
inception of fractal geometry and chaos theory (FGCT)
and which seems to have given us a truly 'reasonable’, i.e., natural, mathematic.
It has to be a matter of intuition, of course,
as proof is a matter of time, but it would seem that in the complex combine of fractal geometry and chaos theory we are possessed
of what might be called 'The Mathematical Principles of Natural Philosophy' (to borrow the Newtonian title)
or 'nature's own geometry'. This is the Philosopher's or the Ionian Dream, most importantly, Descartes'
Dream, to be possessed of the mathematical key by which we might understand the created universe. This is
the dream that has driven the development of science itself, as well as mathematics, underpins the emergence of
our 'Enlightenment' science and has been the philosophic position of centuries of thinkers through from
the Babylonians and Greeks, to Descartes and Einstein. (See pretty much any book by John D Barrow).
Mandelbrot did, after all, go
out and ‘measure the world’, definitively in search of nature’s own geometry, yet much of science seems surprised by, or disbelieving of, the possibility that he might just have done such an incredible thing - including
Mandelbrot himself.
Despite the force of intuition that informs the many who have come to share the dream and find it somehow realised
in FGCT, there are still today mathematicians
and scientists who have not recognised what it is
they in fact have - or are perhaps too modest to try and claim it.
Some have disregarded it believing it
to be a fad or passing fashion. Fashions come and go and the careful academic is reluctant to hope too much of
any particular schema given the propensity for current truths to fall in the light of later findings. Moreover there
is considerable pressure on the working academic to produce results and stay at the top of their field which, once the fashion
is in swing, can only be done by effectively surfing every new fashion, no matter that these requirements distract from focussed
attention on and development of potentially more valuable work.
An excellent example of this type of fashion driven
thinking is given by Philip Ball in his recent series of books on Flow, Shapes and Branches and he effectively gives
verbatim report of just such thinking in operation, saying he:
'can think of no better illustration
than fractals of the fact that science, like any other human activity, is prey to fashion' ... 'In scientific research,
where once it was a matter of interest merely to identify a new fractal structure, this now elicits a weary shrug of the shoulders,
for scientists have grown accustomed to the notion that they are ubiquitous.' One has to wonder why ubiquity speaks so
little to so many scientists? Surely that very ubiquity, that universal expression, is something that indicates something
truly profound and fundamental? He goes on to report the failure of the mathematical community to make the connection
between the fractals and number theory.
'Some mathematicians sniffily dismissed the fad for fractals
as a kind of fancy computer-graphic doodling, nothing to do with their precise and intricate art of numbers.' (Ball,
2009).
One has to suspect that part of the reason for this perception is the developmental history of the mathematic which, after the initial introduction of the coincident conceptions
of Fractal Geometry as the metric and the Feigenbaum, the dynamic signature of chaos, as its iconic
signifier in 1974, was followed in 1980 by the advent of the Mandelbrot Set – ‘the most extraordinary discovery in the history
of mathematics' (A C Clarke, 1989), but ever since has necessarily been wrapped up in self-examination and seemingly unbiquitous application - application
so wide, indeed, as to extend from quantum to cosmos - that even the mathematicians have become 'bored' with
fractality. At base, you have to think, it is just a failure of imagination.
Double Nobel laureate, Ilya Prigogine, at a Holloway College seminar in 1995, made perfectly explicit the transition of vision he had undergone in applying the new mathematic when he spoke of it delivering a perspective
he had never before imagined and how the mathematic
itself indicated the natural direction for future
work. At that time he was making notes for his next book that, he explained, would be a ‘more philosophical tract than usual’ and which he had provisionally
titled as The New Enlightenment. (His announcement was, for this author, music to the ears as a clearly visible envelope sticking out
of his bag by the dias as he spoke contained an outline of the thinking illustrated herein, with suggestion as to
that same title for the work!?)
On stage with Prigogine was John Polkinghorne,
a mathematical physicist, who had earlier proposed:
‘The recognition of structured chaos has
been hailed as a "third revolution", worthy to be set alongside the Newtonian and quantum mechanical revolutions
which preceded it’ (Polkinghorne, 1991).
Indeed,
in his exploration of what the new mathematics has wrought in terms of our understanding of physical systems, he in passing touches upon the subject at the heart of this website:
‘The physical systems
about which I have been talking are complicated, but they fall far short of the complexity of even the simplest living cell [] In an as yet small and imperfect way, one might hope to begin to see some chance of gaining
modest insight into how the levels of physics and
biology might eventually be found to interlock
in their description of the world’.
After nearly thirty years work and exploration the
sheer breadth of application of fractality might be
taken as indicator enough of the fundamental status of the mathematic, but an ever-increasing catalogue of phenomena visited and transformed by FGCT, it seems, will not suffice and signal achievement is now required as confirmation of the
profound status of the new mathematic.
It is hoped that the model outlined here might contribute to such.
It can readily be predicted that future science
will divide around the issue of FGCT as those avoiding
the use and implications of such continue to work in what must become known as the 'classical’ approach, whilst their more accepting colleagues fairly claim to be doing the science of the ‘real’.
Strategically this is anyway necessary for science to continue in questioning all assumptions. It will, of course,
be particularly schismatic for mathematics, but out
of that division of the mathematical realm will emerge an infinitely more beautiful and profound 'natural
mathematics' and, therein, a new, and this time 'real', enlightenment.
|
|
| The now iconographic Feigenbaum and the Mitral valve of the human heart - a mathematic of the real? |
|
|
| How the chaotic input to the ventricle flows and folds to form the mitral valve |
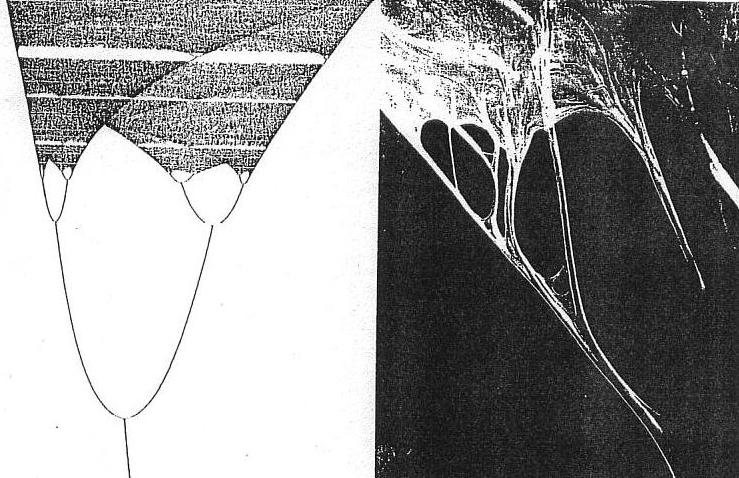
The relations of the Feigenbaum and the Mitral valve (above) are easily analysed
by intuition in so far as we can understand the
evolution of the latter as emerging
out of controlling a chaotic flow. Imagine the component population
of objects
carried in the blood - from huge amoeboid
white cells, the smaller erythrocytes,
large protein array such as fibrinogens
and massive molecules such as hormones,
through to the fine array of circulating peptides of various sizes, e.g., penta-,
hexa-, nonapeptides, etc., all incident
upon this controlling vane. Their different
masses, tumbling flow dynamics and pulse-driven arrival present a population
of objects that constitute as good a chaos as might be found anywhere.
Naturally,
it seems, you best control chaos with chaos. The valve acts as chaotic
attractor
and sink, before then
acting as chaotic source or impeller to drive the flow.
|
|
| Stained cell: green - actin, red - nuclear protein |
|
|
| Computer rendered 5 dimensional M Set |
Would the mathematicians
really choose to suggest that the new mathematics cannot describe
all natural systems?
The cell (above, left) and the M Set rendering (right)
present us with more than just an apparent correlation.
At the heart of the M Set is a virtual perfect
platonic sphere, similar to the nucleus of the cell, and the M Set is what happens when you place within it the Feigenbaum, the signature of chaos
and disequilibrium. Disequilibrium is everything and sets the dynamic frame for flow
between source and sink.
Transcendent mathematics
History seems to have taken a strange turn in so far as the present circumstances indicate that we
are returned to something like the pre-Enlightenment world and the last few centuries will come to be seen as childish
prelude to what now is emerging as the new science founded in a new mathematic.
It may well be that
the mathematicians do not dare declare 'revolution' because you know that the one thing that
must emerge is something new. Perhaps they cannot face having to discover a new mathematic when it
must be discovered by other means than usual and changes the mathematician's role from that of exploring the
nature of number to one of seeking to understand the number of nature?
Fractal geometry is of course
immensely powerful, that power deriving from the transcendence of phenomenogical realms which it allows as both
conceptual device and mathematical metric, equally and, in that, is born its poetry. Subtle, simple, beautiful
and infinite are other terms that begin to find more profound meaning - as though they are not already profound
enough.
Indeed, although it is to us, to man's mind, a new mathematic, we discover of course that it
is the only geometry natural creation has ever worked with or, perhaps, been worked by - at least until the
advent of man. It then becomes not a new mathematic, but a literally profound one.
There
are a lot of poetic minded scientists, some not even so minded until they took to science, and it seems they are
at last to have their chance to speak. The poetic or revelatory nature of the new science is underpinned by the
fact of the iconographic signifier of the new mathematic - the Mandelbrot Set - being also, very literally,
the object of our dreams (or of mine and Descartes' at least), a mathematical 'mother object' that holds
- or rather itself is - the key to nature's own geometry. The mathematical Rosetta
Stone.
|
|
| Fractal scale invariance - at quantum, meso and cosmic scales - requires a transcendent mathematic |
Working with paradox
Just as making the case for living systems as the purest quantum systems is
a paradoxical approach, so too we can examine the larger proposal thereby entailed, which is that of this indeed
being a fractal universe, by immediately moving to that extreme position, i.e., where we accept the premise of a
fractal universe and see how far that thinking gets us.
If, then, we are to explore the emergence of
life and, therein, man within a fractal universe, we most immediately need to establish the recurrence
of pattern at many scales of length and time. An example of just such scaled phenomenological recurrence was
given on the opening page and is given above.
We have fractal geometry of course to give us all the various measures
within each phenomenal level, but for moving between levels and characterising the pattern recurrence of any particular
level, we naturally require an array of scale invariant or transcendent mathematical objects or operators.
This requirement then naturally aligns current mathematical need with that which was desired and begun by Leibniz
in his identification of the natural scale invariant operators - unity (1), e and pi - as 'transcendental numbers'.
Then too, of course, he introduced the fourth transcendental operator, i, the imaginary.
The natural appearance
here of Leibnizian thinking, as is in fact now necessitated by the possibility of quantum description of living systems
operation, chimes with the thought again of a great arc of theory turning through the 'Enlightenment' and only
now returning to where, by the accident of history, the arc began to build away from a better theoretic. How very
very different science today might have been had history accepted Leibniz as the prime mathematic visionary rather than,
as things in fact played out, Newton. There is not room enough or time here to spell out the essential shortfall of
the 'Newtonian revolution' except in so far as to wonder at when teaching by exception ends and dealing with
the actual begins. Newtonian physics should always be presented with the motto 'Exactly the way the
world doesn't work'.
In the application of physics to living systems, it is certainly the
approach of Leibniz that best informs. This is beautifully and simply illustrated by comparison of the thinking
of Leibniz, Einstein and Eddington on tables. Let either of the latter sit at a table and we hear of their visions of
fuzzy, fizzing quanta and atoms, the real physics they imagine underpinning the natural worked form of the wood.
To Leibniz, however, it is a 'colony of souls', in which poetic expression he voices one of the most testing of
phenomena for any science, the generation of mind and, within that, self. He poetically expresses what science still
today seeks to understand and that is how the properties of 'dull matter' are by living systems working transformed
such as to enable the emergence of consciousness.
Today, by dint of fractal geometry and chaos theory, we
might just as likely call Leibniz's transcendental measures 'scale invariant', which description, of
itself, bespeaks a necessarily transcendent nature.
In order, therefore, to understand the phenomena generated
within such a transcendently defined universe, we expect that by working with only that which is 'given' we
can still construct a mathematic that recognises the working of chaos and, like Prigogine, accepts the 'end
to certainty' necessarily entailed.
When it comes to development of the new mathematical
realm we need to change our understanding of numbers beyond unity. By this it is meant that the discrete integers
or 'real' numbers are in fact no such thing, whilst the operators noted as transcendent or even imaginary in
classical mathematics are the 'reals' for the new mathematic.
HOW DID IT ALL GO SO WRONG ...?
In the
immediate circumstance, it would seem that the mathematicians are themselves most to blame for having missed in 1974 the significance
of the co-incident characterisation of both the fundamental metric and the dynamic natural measures that are embodied
in, respectively, fractal geometry and chaos theory, and for which the Mandelbrot Set and the Feigenbaum are today iconographic.
In the longer term mathematics seems to have still not yet taken on board the relativistic reality that underpins
the co-ordinate geometry of Descartes and makes obsolete the considerations of the classical mathematics of such as Russell
and Whitehead in considering arithmetic and the proof required for such theoretical constructs as 1 + 1 = 2.
|